Mathematics

Mathematics includes the study of such topics as quantity (number theory), structure (algebra), space (geometry), and change (mathematical analysis). It has no generally accepted definition.

• https://es.wikipedia.org/wiki/Matem%C3%A1ticas
• https://en.wikipedia.org/wiki/Mathematics#cite_note-Mura-7

• Number theory (or arithmetic)

https://en.wikipedia.org/wiki/Number_theory

https://www.math.brown.edu/~jhs/frintch1ch6.pdf

• Algebra https://en.wikipedia.org/wiki/Algebra

• Linear algebra https://en.wikipedia.org/wiki/Linear_algebra

Linear algebra is the branch of mathematics concerning linear equations, linear maps, and their representations in vector spaces and through matrices.

• Geometry https://en.wikipedia.org/wiki/Geometry

• Mathematical analysis (Math of change) https://en.wikipedia.org/wiki/Mathematical_analysis

• Analytic geometry https://en.wikipedia.org/wiki/Analytic_geometry

• Infinitesimal calculus (Math of change) (The study of things that change) https://en.wikipedia.org/wiki/Calculus

https://www.youtube.com/watch?v=w3GV9pumczQ

• Differential calculus (Derivative) https://en.wikipedia.org/wiki/Differential_calculus

• Integral calculus https://en.wikipedia.org/wiki/Integral

• Fundamental theorem of calculus https://en.wikipedia.org/wiki/Fundamental_theorem_of_calculus

• One of the applications of Mathematical analysis (Calculus in particular) is for Signal processing

• Applied mathematics: Some disciplines are considered to be applied mathematics. Sin embargo, no me queda claro si las área que estoy enumerando aquí realmente forman parte de lo que se conoce como Applied mathematics. En particular, Statistics can be considered to be a distinct mathematical science rather than a branch of mathematics. https://en.wikipedia.org/wiki/Statistics

• Discrete mathematics https://en.wikipedia.org/wiki/Discrete_mathematics

• Numerical analysis https://en.wikipedia.org/wiki/Numerical_analysis

• Computer algebra https://en.wikipedia.org/wiki/Computer_algebra

• Statistics https://en.wikipedia.org/wiki/Statistics

• Applications of mathematics:

• Signal processing:

One of the applications of Mathematical analysis (Calculus in particular) is for Signal processing.

When processing signals, such as audio, radio waves, light waves, seismic waves, and even images, Fourier analysis can isolate individual components of a compound waveform, concentrating them for easier detection or removal. A large family of signal processing techniques consists of Fourier-transforming a signal, manipulating the Fourier-transformed data in a simple way, and reversing the transformation. https://en.wikipedia.org/wiki/Mathematical_analysis#Signal_processing

• Time-frequency analysis https://en.wikipedia.org/wiki/Time%E2%80%93frequency_analysis

• Fourier transform https://en.wikipedia.org/wiki/Fourier_transform

• Seismic processing

• Time-frequency analysis in Seismic processing:

A set of mathematical formulas used to convert a time function, such as a seismic trace, to a function in the frequency domain (Fourier analysis) and back (Fourier synthesis). The Fourier transform is used extensively in signal processing to design filters and remove coherent noise. Many filtering operations are performed in the frequency domain. The Fourier transform has applications in image analysis and in pattern recognition in geological systems. https://www.glossary.oilfield.slb.com/en/Terms/f/fourier_transform.aspx#:~:text=A%20set%20of%20mathematical%20formulas,and%20back%20(Fourier%20synthesis).&text=The%20Fourier%20transform%20is%20used,filters%20and%20remove%20coherent%20noise.

Numbers

https://en.wikipedia.org/wiki/Real_number

Real numbers ($\mathbb {R}$) include the rational numbers ($\mathbb {Q}$), which include the integers ($\mathbb {Z}$), which in turn include the natural numbers ($\mathbb {N}$)

• $\mathbb {R}$: A real number is a value of a continuous quantity that can represent a distance along a line (or alternatively, a quantity that can be represented as an infinite decimal expansion). https://en.wikipedia.org/wiki/Real_number

• $\mathbb {Q}$: A rational number is a number that can be expressed as the quotient or fraction $p/q$ of two integers, a numerator $p$, and a non-zero denominator $q$. https://en.wikipedia.org/wiki/Rational_number

• Numbers like ${\sqrt {2}}$ or $\pi$ cannot be expressed as the ratio of two integers, but can be represented on real number line. https://socratic.org/questions/what-is-the-difference-between-real-numbers-and-rational-numbers

What is a function

https://en.wikipedia.org/wiki/Function_(mathematics)

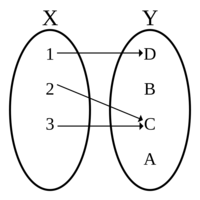
Diagram of a function, with domain $X={1,2,3}$ and codomain $Y={A,B,C,D}$, which is defined by the set of ordered pairs ${(1,D),(2,C),(3,C)}$. The image/range is the set ${C,D}$ . Taken from https://en.wikipedia.org/wiki/Function_(mathematics)

• In mathematics, a function is a binary relation over two sets that associates every element of the first set, to exactly one element of the second set.

• Intuitively, a function is a process that associates each element of a set $X$, to a single element of a set $Y$.

• Formally, a function $f$ from a set $X$ to a set $Y$ is defined by a set $G$ of ordered pairs $(x,y)$ such that $x\in X$ and $y\in Y$.

• $X$ and $Y$ are respectively called the domain and the codomain of the function $f$

• $G$ is called the graph of the function. In mathematics, the graph of a function $f$ is the set of ordered pairs $(x,y)$, where $f(x)=y$.

• In mathematically we usually write $y=f(x)$

• We say $y$ is a function of $x$

• Which means that mathematically $y$ depends on $x$.

• So, as in this case, the independent variable is often designated by $x$. The dependent variable is often designated by $y$.

• A basic example of a function: Linear Functions: https://en.wikipedia.org/wiki/Linear_function

$f(x)=ax+b$

$y=ax+b$

Where $a$ and $b$ are constants. $a$ is frequently referred to as the slope of the line, and $b$ as the intercept.

$x$ and $y$ $\in$ ℝ

$y=-x+5$ $x$ $y$ 0 5 1 4 2 3 3 2 4 1 5 0 6 -1 7 -2 8 -3 9 -4

}

Continuity

A rigorous definition of continuity of real functions is usually given in a first course in calculus in terms of the idea of a limit. First, a function f with variable x is said to be continuous at the point c on the real line, if the limit of f(x), as x approaches that point c, is equal to the value f(c); and second, the function (as a whole) is said to be continuous, if it is continuous at every point. A function is said to be discontinuous (or to have a discontinuity) at some point when it is not continuous there. These points themselves are also addressed as discontinuities. https://en.wikipedia.org/wiki/Continuous_function

A sequence of continuous functions fn(x) whose (pointwise) limit function f(x) is discontinuous. The convergence is not uniform. https://en.wikipedia.org/wiki/Continuous_function

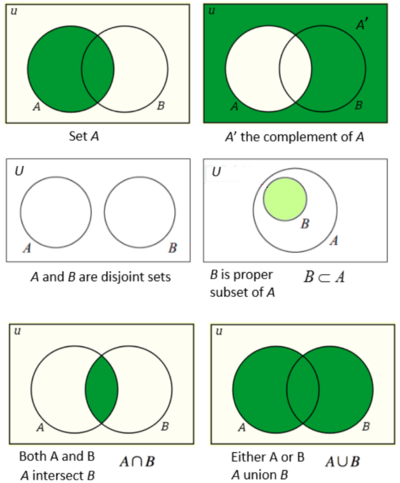
Set Operations - Union, Intersection, Complement

Taken from https://www.onlinemathlearning.com/union-set.html