Mathematics
Revision as of 17:22, 5 September 2020 by Adelo Vieira (talk | contribs)
Mathematics includes the study of such topics as quantity (number theory), structure (algebra), space (geometry), and change (mathematical analysis). It has no generally accepted definition. https://en.wikipedia.org/wiki/Mathematics#cite_note-Mura-7
- Number theory (or arithmetic) https://en.wikipedia.org/wiki/Number_theory
- Linear algebra https://en.wikipedia.org/wiki/Linear_algebra
- Linear algebra is the branch of mathematics concerning linear equations, linear maps, and their representations in vector spaces and through matrices.
- Mathematical analysis (Math of change) https://en.wikipedia.org/wiki/Mathematical_analysis
- Analytic geometry https://en.wikipedia.org/wiki/Analytic_geometry
- Infinitesimal calculus (Math of change) (The study of things that change) https://en.wikipedia.org/wiki/Calculus
- Differential calculus (Derivative) https://en.wikipedia.org/wiki/Differential_calculus
- Integral calculus https://en.wikipedia.org/wiki/Integral
- Fundamental theorem of calculus https://en.wikipedia.org/wiki/Fundamental_theorem_of_calculus
- One of the applications of Mathematical analysis (Calculus in particular) is for Signal processing
- Applied mathematics: Some disciplines are considered to be applied mathematics. Sin embargo, no me queda claro si las área que estoy enumerando aquí realmente forman parte de lo que se conoce como Applied mathematics. En particular, Statistics can be considered to be a distinct mathematical science rather than a branch of mathematics. https://en.wikipedia.org/wiki/Statistics
- Discrete mathematics https://en.wikipedia.org/wiki/Discrete_mathematics
- Numerical analysis https://en.wikipedia.org/wiki/Numerical_analysis
- Computer algebra https://en.wikipedia.org/wiki/Computer_algebra
- Statistics https://en.wikipedia.org/wiki/Statistics
- Applications of mathematics:
- Signal processing:
- One of the applications of Mathematical analysis (Calculus in particular) is for Signal processing.
- When processing signals, such as audio, radio waves, light waves, seismic waves, and even images, Fourier analysis can isolate individual components of a compound waveform, concentrating them for easier detection or removal. A large family of signal processing techniques consists of Fourier-transforming a signal, manipulating the Fourier-transformed data in a simple way, and reversing the transformation. https://en.wikipedia.org/wiki/Mathematical_analysis#Signal_processing
- Time-frequency analysis https://en.wikipedia.org/wiki/Time%E2%80%93frequency_analysis
- Fourier transform https://en.wikipedia.org/wiki/Fourier_transform
- Seismic processing
- Time-frequency analysis in Seismic processing:
- A set of mathematical formulas used to convert a time function, such as a seismic trace, to a function in the frequency domain (Fourier analysis) and back (Fourier synthesis). The Fourier transform is used extensively in signal processing to design filters and remove coherent noise. Many filtering operations are performed in the frequency domain. The Fourier transform has applications in image analysis and in pattern recognition in geological systems. https://www.glossary.oilfield.slb.com/en/Terms/f/fourier_transform.aspx#:~:text=A%20set%20of%20mathematical%20formulas,and%20back%20(Fourier%20synthesis).&text=The%20Fourier%20transform%20is%20used,filters%20and%20remove%20coherent%20noise.
- Real numbers () include the rational numbers (Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \mathbb{Q}} ), which include the integers (Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \mathbb{Z}} ), which in turn include the natural numbers (Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \mathbb{N}} )
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \mathbb{R}} : A real number is a value of a continuous quantity that can represent a distance along a line (or alternatively, a quantity that can be represented as an infinite decimal expansion). https://en.wikipedia.org/wiki/Real_number
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \mathbb{Q}} : A rational number is a number that can be expressed as the quotient or fraction Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle p/q} of two integers, a numerator Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle p} , and a non-zero denominator Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle q} . https://en.wikipedia.org/wiki/Rational_number
- Numbers like Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \sqrt{2}} or Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \pi} cannot be expressed as the ratio of two integers, but can be represented on real number line. https://socratic.org/questions/what-is-the-difference-between-real-numbers-and-rational-numbers
- What is a function: https://en.wikipedia.org/wiki/Function_(mathematics)
- In mathematics, a function is a binary relation over two sets that associates every element of the first set, to exactly one element of the second set.
- Intuitively, a function is a process that associates each element of a set Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle X} , to a single element of a set Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle Y} .
- Formally, a function Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle f} from a set Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle X} to a set Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle Y} is defined by a set Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle G} of ordered pairs Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle (x, y)} such that Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle x \in X} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle y \in Y} .
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle X} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle Y} are respectively called the domain and the codomain of the function Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle f}
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle G} is called the graph of the function. In mathematics, the graph of a function Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle f} is the set of ordered pairs Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle (x, y)} , where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle f(x) = y} .
- In mathematically we usually write Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle y = f(x)}
- We say Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle y} is a function of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle x}
- Which means that mathematically Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle y} depends on Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle x} .
- So, as in this case, the independent variable is often designated by Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle x} . The dependent variable is often designated by Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle y} .
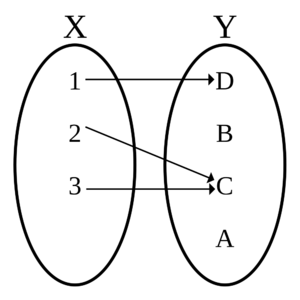
- Diagram of a function, with domain Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle X = {1, 2, 3}} and codomain Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle Y = {A, B, C, D}} , which is defined by the set of ordered pairs Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {(1, D), (2, C), (3, C)}} . The image/range is the set Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle {C, D}}
- A basic example of a function: Linear Functions: https://en.wikipedia.org/wiki/Linear_function
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle f(x) = ax + b}
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle y = ax + b}
- Where Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle b} are constants. Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle a} is frequently referred to as the slope of the line, and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle b} as the intercept.
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle x} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle y} Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://en.wikipedia.org/api/rest_v1/":): {\displaystyle \in} ℝ
- Graphs of two linear functions.
- Graphs of two linear functions.