Data Structures & Algorithms

What is Data Structure?

Diferentes definiciones:

1. A data structure is the logical or mathematical model of a particular organization of data.
2. A data structure is a way to logically organize data that specifies:
   • A set of data elements i.e., a data object and,
   • A set of operations which may legally be applied to elements of this data object.
3. A data structure is a method of organizing information so that the information can be stored and retrieved efficiently.

• A data structure not only stores data, but also supports the operations for manipulating data in the structure.

• For example, an array is a data structure that holds a collection of data in a sequential order. You can find the size of the array, store, retrieve, and modify data in the array.
  • An Array is simple and easy to use, but it has two limitations:
    • Once an array is created, its size cannot be altered.
    • Array provides inadequate support for inserting, deleting, sorting, and searching operations.

Applications of Data Structure

• Graphics
• Compiler Construction
• Database Management Systems
• Numerical Analysis
• Simulations
• Statistical analysis package
• Financial Modelling
• Artificial Intelligence

Two categories of data structures

Linear data structures

• ArrayList is a linear collection of entries in which entries may be added, removed, and searched for without restrictions.
• Queue:

• Entries may only be removed in the order in which they are added.

• First out (FIFO) data structures
• No search for an entry in the Queue

• Stack:

• Entries may only be removed in the reverse order in which they are added.

• Last In, First Out (LIFO)
• No search for an entry in the Stack.

• Heap as a Priority Queue:

• A priority queue is a specialization of the FIFO Queue.
• Entries are assigned priorities.
• The entry with the highest priority is the one to leave first.

Nonlinear data structures

• Trees
• Binary Tree
  • Consists of entries each of which contributes to the tree as a whole based on its position in the tree.
  • Moving an entry from one position to another changes the meaning of the Binary Tree.
• General Tree
  • Models a hierarchy such as the organizational structure of a company, or a family tree.
  • A non-linear arrangement of entries, it is a generalization of the binary tree structure, hence the name.
• Hash Table
• Graphs

Data Structures in Java

Several data structures provided by the Java utility packages and the major DS are:

• Enumeration: It allows retrieval of successive elements from other data structures (acts as an interface).

• BitSet: Collection of bits (used as flags) with the ability to set or clear as appropriate.

• Vector: Variable length array (dynamic array).

• Stack: Collection of objects with a defined order.

• Dictionary: Dictionary (map, association list) is a data structure, which is generally an association of unique keys with some values. We can bind a value to a key, delete a key (and naturally an associated value) and lookup for a value by the key.

• Hashtable: Hashtable stores key/value pairs in a hash table. Keys are used to specify the objects along with their link to values. The keys are hashed and resulting hash code is used as the index at which the value is stored within the table.

• Properties: Properties is a subclass of Hashtable. It is used to maintain the list of values in which the key is a String and the value is also a String.

What is an algorithm?

• An algorithm is a sequence of unambiguous instructions for solving a problem, i.e., for obtaining a required output for any legitimate input in a finite amount of time.
• The algorithms are independent of programming languages.

Five Features of Algorithm

• Finiteness: An algorithm must always terminate after a finite number of steps. Similar procedures which differ only in that they do not terminate can be described as computational methods.

• Definiteness: Each step of an algorithm must be precisely defined; the actions to be carried out must be rigorously and unambiguously specified for each case.

• Input: An algorithm has zero or more inputs: quantities that are given to it initially before the algorithm begins, or dynamically as the algorithm runs.

• Output: An algorithm has one or more outputs: quantities that have a specified relation to the inputs.

• Effectiveness: An algorithm is also generally expected to be effective, in the sense that its operations must all be sufficiently basic that they can in principle be done.

Correctness and Efficiency

What do we need?: Correctness and Efficiency

Correctness can be described as:

• We can be more confident in the logic behind our programs if we can be sure of and agree on the logic of the data structures used
• A given data structure has defined access and modification methods

Efficiency can be considered in terms of multiple resources:

• These include time and space considerations
• We will mostly consider time but at times we may have to compromise with regard to space

Maintainable Code

We need to take the following into account:

• Long functions:
  • Long functions can complicate the code
  • It becomes unclear what the purpose of the function is
  • Additionally, it is difficult to debug longer functions
  • Distribute the load of programming logic into small parts to obtain better efficiency

• Multiple responsibilities:
  • Across the board, ensure that the methods, classes and modules are only responsible for what they need to be responsible for.
  • For example, the same class should not process data, display data, and handle I/O.
  • High Cohesion = clearly defined responsibility.

• Don't repeat yourself
  • If the same code is in multiple places, then updates need to be applied to all locations.
  • Calling a suitable function rather than inserting a block of code increases legibility.

• Naming conventions
  • Consider names as a form of documentation.
  • Selecting good names and following a specific style makes everyone's life easier.
  • For both naming conventions and code style we will be following the Google Style guides throughout this course.

Naming conventions in java

• Use assertions
  • Assertions are very useful for both:
    • Debugging and
    • In-code documentation

public int divide(int i, int j){
    ASERT (J>0);
    return i/j;
}

• Refactoring

• Testing

Classes of algorithms on data structures

• Search
• Sort
• Insert
• Update
• Delete

Analysis of algorithms

• The area of computer science that provides tools for contrasting efficiency of different algorithms
• We consider comparisons of algorithms, not programs

Algorithm analysis should be independent of Specific implementations, computers, and data.

• Difficulties with comparing programs (instead of algorithms):

• How are the algorithms coded
• What computer will be used
• What data should the program use

• How good is the algorithm?
  • Time efficiency
  • Space efficiency

• Does there exist a better algorithm?
  • Lower bounds
  • Optimality

Methods to analyze an algorithm

• Transform the algorithm into some programming language and measure the execution time for a set of input values.
• Use the Big O notation (mathematical notation) to analyse the behaviour of the algorithms. (Independent of software and hardware).

Big-Oh Notation

• Big-O notation expresses the performance of an algorithm as a function of the number of items to be processed
• This permits algorithms to be compared for efficiency

Analyzing Loop Execution:

• First determine the order of the body of the loop, then multiply that by the number of times the loop will execute
• N loop executions times O(1) operations results in a O(n) efficiency

count = 1;                            // O(1)
while (count < n)                     // n times  
{
    count *= 2;                       // O(2)
    // some sequence of O(1) steps
}

• O(1) * n * O(2)
• n * O(2) because it is constant
• n * O(1)
• O(n)
• The loop is executed n times, so the loop is O(n)

Nested loops:

for (int count = 0; count < n; count++) {
    for (int count2 = 0; count2 < n; count2++) {
        // Some sequence of O(1) steps
    }
}

• When the loops are nested, we multiply the complexity of the outer loop by the complexity of the inner loop
• Both the inner and outer loops have complexity of O(n)
• The overall efficiency is O(n^2)

• The body of a loop may contain a call to a method
  • To determine the order of the loop body, the order of the method must be taken into account
  • The overhead of the method call itself is generally ignored

for (int i = 0; i < n; i++) {        //------
    for (int j = 0; j < n; j++) {    //
        Simple Statement             //  This nested loop executes a Simple Statement  n^2  times
    }                                //
}                                    //------
for (int i = 0; i < n; i++) {        //------
    Simple Statement  1              //
    Simple Statement 2               //
    Simple Statement 3               // This loop executes 5 Simple Statements  n times (5n)
    Simple Statement 4               //
    Simple Statement 5               //
}                                    //------
Simple Statement 6                   //------ 
Simple Statement 7                   // Finally, 25 Simple Statements  are executed
...                                  //
Simple Statement 30                  //------ 

// We can conclude that the relationship between processing time and n (the number of date items processed)  is:
// T(n) = n^2 + 5n + 25

An O(n) algorithm

for i = 1 to n
    sum = sum + i

An O(n^2) algorithm

for i = 1 to n
    for i = 1 to n
        sum = sum + i

Some examples

Find the complexity of the following functions and source code provided in the following questions:

• 6n^2 + 3
  • Sol: O(n^2)

• n2 + 17n + 1
  • Sol: O(n^2)

• 5n^3 + 100n^2 - n - 10
  • Sol: O(n^3)

• 3n^2 + 2^n
  • Sol: O(2^n)

• Order the following growth rates from smallest to largest:

n2    n!    n log n    2n    n     log n 

Sol: log n     n     n log n     2n     n2     n!

• Given f(n) = 4n + 63 + 5n^2 + 3n log n what is g(n)?
  • g(n) = (n^2) (the dominant term)

• If an algorithm requires 7 basic operations for an algorithm with a problem size of n, the algorithmic complexity is:

a) O(1) (opción correcta)

b) O(7)

c) O(n)

d) O(7n)

• 8) What is the order of the expression 5nlog(5n)?
  • Sol: n log(n)

• In terms of n, what is the running time of the following algorithm to compute x^n:

public static double power( double x, int n ) {
    double result = 1.0;

    for( int i = 0; i < n; i++ )
        result *= x;

    return result;
}

• Sol: The running time is O(n)

• based on this program:

55 1  for (int i = 0 ; i < n ; i++)
56 2      for (int j = i ; j <= n ; j++)
57 3           for (int k = i ; k <= j ; k++)
58 4                sum++;
59 5  for (int p = 0 ; p < n*n ; p++)
60 6      for (int q = 0 ; q < p ; q++)
61 7           sum-;

• How many times is statement 4 executed?

• Sol: O(n^3)

• How many times is the statement 7 executed?

• Sol: O(n^4)

• What is the running time of the fragment?

• Sol: O(n^4)

Asymptotic Analysis

Asymptotic Performance

Asymptotic Performance

The Stack Data Structure

Stack Abstract Data Type

• A stack is one of the most commonly used data structures in computer science
• A stack can be compared to a Pez dispenser
  • Only the top item can be accessed
  • You can extract only one item at a time

• A stack is a linear collection whose elements are added in a last in, first out (LIFO) manner:
  • This means that the last element to be put on a stack is the first one to be removed.

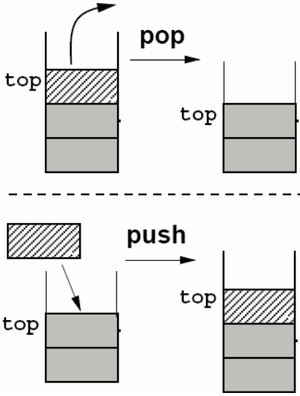
• Push: Add an entry to the top of the stack
• Pop: Delete the entry at the top of the stack

Stack operations

Main operations:

• object push(): Inserts an element
• object pop(): Removes and returns the last inserted element

Auxiliary operations:

• object peek() or top(): Returns the last inserted element without removing it
• integer size(): Returns the number of elements stored
• boolean isEmpty(): Indicates whether no elements are stored

Example and applications of Stack

• Surfing the Web on a browser:
  • The sequence of back clicks loads the browser with Web pages in reverse order of visit.
  • The last visited page is the first loaded when going back.

Direct applications:

• Undo sequence in a text editor
• Chain of method calls in the Java Virtual Machine

Indirect applications:

• Auxiliary data structure for algorithms
• Component of other data structures

Implementing an Array-based Stack in Java

StackInterface.java

public interface StackInterface <E> {
    public void push(E item);
    public E pop();
    public E peek();
    public int size();
    public boolean isEmpty();
    public void StackElements();
}

Stack.java

import java.util.ArrayList;
import java.util.EmptyStackException;

public class Stack<E> implements StackInterface<E> {
    
    private ArrayList<E> StackList;
    
    public Stack() {
        StackList = new ArrayList<E>();
    }

    // push: Inserts an element
    public void push(E item) {
        if (StackList.size() == 100)
           throw new FullStackException();
        else
           StackList.add(item);
    }
    
    // pop: Removes and returns the last inserted element
    public E pop() {
        if (!isEmpty())
            return StackList.remove(size()-1);
        else
            throw new EmptyStackException();
    }
    
    // peek: Returns the last inserted element without removing it
    public E peek() {
        if (!isEmpty())
            return StackList.get(size()-1);
        else
            throw new EmptyStackException();
    }
    
    // size: Returns the number of elements stored
    public int size() {
        return StackList.size();
    }
    
    // isEmpty: Indicates whether no elements are stored
    public boolean isEmpty() {
        return (StackList.size() == 0);
    }
    
    // StackElements: Print the stack
    public void StackElements() {
        for (int i = 0; i < StackList.size(); i++)
            System.out.println("StackList[" + i + "] = " + StackList.get(i));
    }
    
}

StackImplementation.java

public class StackImplementation {

    public static void main(String[] args) {
        StackInterface DemoStack = new Stack();
        System.out.println("Stack is empty is " + DemoStack.isEmpty());
        DemoStack.push("First Element");
        DemoStack.push("Second Element");
        DemoStack.push("Third Element");
        DemoStack.push("Fourth Element");
        System.out.println("Stack is empty is " + DemoStack.isEmpty());
        System.out.println("Stack elememtns are \n ");
        DemoStack.StackElements();

        DemoStack.pop();
        System.out.println("Size of Stack is " + DemoStack.size());
        //DemoStack.StackElements();
        System.out.println("Peek/top of Stack is " + DemoStack.peek());
        
    }
    
}

FullStackException.java

public class FullStackException extends RuntimeException{
   // no-argument constructor
   public FullStackException(){
      this( "Stack is full" );
   } // end no-argument FullStackException constructor

   
   // one-argument constructor
   public FullStackException( String exception ){
      super( exception );
   } // end one-argument FullStackException constructor
} // end class FullStackException

The Queue Data Structure

The Queue ADT

Properties:

• The Queue ADT stores arbitrary objects.
• Queues are FIFO data structures. Insertions and deletions follow the first-in first-out scheme. All insertions are done at the rear and all deletions at the front.
• The queue has a fixed upper bound (capacity) on the number of elements it can store.

Attributes:

• capacity: The maximum number of elements that can be in the queue at one time.
• size: The number of elements in the queue: 0 ≤ size ≤ capacity at all times.
• front: The first element of the queue or a null value not part of the queue when the queue is empty.
• rear: The position in the queue where the next element is to be inserted or a null value not part of the queue if the queue is full.

Queue operations

Main queue operations:

• enqueue(object): inserts an element at the end of the queue
• object dequeue(): removes and returns the element at the front of the queue

Auxiliary queue operations:

• object firstElement(): returns the element at the front without removing it
• integer size(): returns the number of elements stored
• boolean isEmpty(): indicates whether no elements are stored

Boundary cases:

• Attempting the execution of dequeue or first on an empty queue returns null

Applications of Queues

Direct applications:

• Waiting lists, bureaucracy
• Access to shared resources (e.g., printer)
• Multiprogramming

Indirect applications:

• Auxiliary data structure for algorithms
• Component of other data structures

Implementing an Array-based Queue in Java

• Using an array to store elements of a queue, such that the first element inserted, “A”, is at cell 0, the second element inserted, “B”, at cell 1, and so on.

QueueInterface.java

public interface QueueInterface <E> {
    public void enqueue(E item);
    public E dequeue();
    public E firstElement();
    public int size();
    public boolean isEmpty();
    public void QueueElements();
}

Queue.java

import java.util.ArrayList;

public class Queue <E> implements QueueInterface<E> {
    
  private ArrayList<E> QueueList;
 
	public Queue() {
            QueueList = new ArrayList<E>();
 	}
 
	public void enqueue(E item) {
            QueueList.add(item);
 	}
 
	public E dequeue() {
            if (!isEmpty())
                return QueueList.remove(0);
            else
                throw new EmptyQueueException();
 	}
 
	public boolean isEmpty() {
            return (QueueList.size() == 0);
 	}
	
	public E firstElement() {
            if (!isEmpty())
                return QueueList.get(0);
            else
                throw new EmptyQueueException();
 	}
 
	public int size() {
            return QueueList.size();
 	}
 
	
	public void QueueElements() {
            for (int i = 0; i < QueueList.size(); i++)
                System.out.println("QueueList[" + i + "] = " + QueueList.get(i));   
 	}
        
}

QueueImplementation.java

public class QueueImplementation {

    public static void main(String[] args) {
        QueueInterface DemoQueue = new Queue();
        System.out.println("Queue is empty is " + DemoQueue.isEmpty());
        DemoQueue.enqueue("First Element");
        DemoQueue.enqueue("Second Element");
        DemoQueue.enqueue("Third Element");
        DemoQueue.enqueue("Fourth Element");
        System.out.println("Queue is empty is " + DemoQueue.isEmpty());
        System.out.println("Queue elememtns are \n ");
        DemoQueue.QueueElements();

        DemoQueue.dequeue();
        System.out.println("Size of Queue is " + DemoQueue.size());
        //DemoQueue.QueueElements();
        System.out.println("Peek/top of Queue is " + DemoQueue.firstElement());
    }
    
}

EmptyQueueException.java

import java.lang.Exception;

public class EmptyQueueException extends RuntimeException { 
    public EmptyQueueException() { super(); } 
    public EmptyQueueException(String msg) { super(msg); }
}

Priority Qeueus ADT

• Recall that a FIFO queue removes elements in the order in which they were added.
• A priority queue removes elements in priority order, independent of the order in which they were added
• Priority queues can be implemented by using arrays, linked list and heap.
• A priority queue stores a collection of entries. Each entry is a pair (key, value)

• Applications:
  • Standby flyers
  • Auctions
  • Stock market

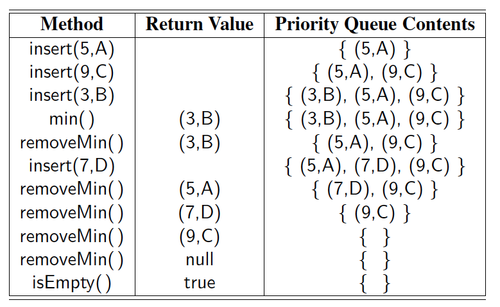
• Main methods of the Priority Queue ADT:
  • insert(k, x) : Inserts an entry with key k and value x
  • removeMin()  : removes and returns the entry with smallest key

• Additional methods:
• min() : returns, but does not remove, an entry with smallest key
• size()
• isEmpty()

• Example - A sequence of priority queue methods:

A sequence of priority queue methods

Entry ADT

• An entry in a priority queue is simply a key-value pair.
• Priority queues store entries to allow for efficient insertion and removal based on keys.

Methods:

• getKey: returns the key for this entry
• getValue: returns the value associated with this entry

As a Java interface:

/** 
  * Interface for a key-value
  * pair entry 
 **/
public interface  Entry<K,V> {
     K getKey();
     V getValue();
}

PriorityQueue Java Class

Java provides a PriorityQueue<E> class that implements the Queue<E>' interface.

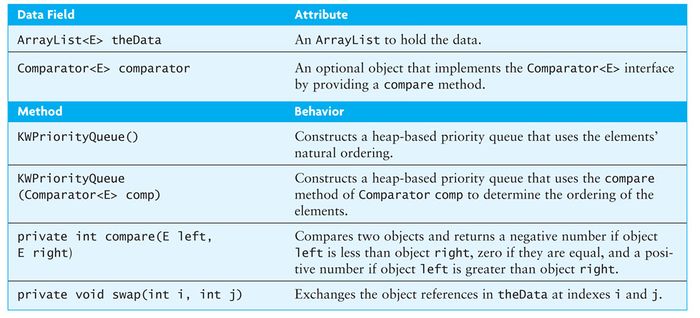
Using a Heap as the Basis of a Priority Queue

• In a priority queue, just like a heap, the smallest item always is removed first.
• Because heap insertion and removal is O(log n), a heap can be the basis of a very efficient implementation of a priority queue.
• While the java.util.PriorityQueue uses an Object[] array, we will use an ArrayList for our custom priority queue, KWPriorityQueue
• In a heap, the highest (or lowest) priority element is always stored at the root. A heap is not a sorted structure and can be regarded as partially ordered.

Design of a KWPriorityQueue Class

The Array Data Structure

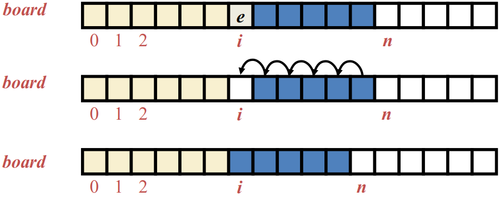
An array is a sequenced collection of variables all of the same type. Each variable, or cell, in an array has an index, which uniquely refers to the value stored in that cell. The cells of an array, A, are numbered 0, 1, 2, and so on. Each value stored in an array is often called an element of that array.

• An array can store primitive elements, such as characters.
• An array can also store references to objects.

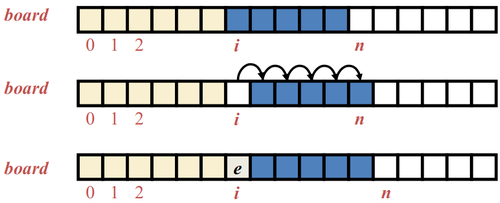
• Adding an Entry:
  • To add an entry e into array board at index i, we need to make room for it by shifting forward the n - i entries board[i],...,board[n - 1]

• Removing an Entry:
  • To remove the entry e at index i, we need to fill the hole left by e by shifting backward the n - i - 1 elements board[i + 1],...,board[n - 1]

The List Data Structure

The List ADT https://www.youtube.com/watch?v=HdFG8L1sajw

List as Abstract Data Type. Cuando hablamos de ADT, queremos simplemente definir el comportamiento de la estructura de datos que queremmos; y no la definición estricta de una implementación en programación. Por tanto, en este sentido, a List ADT sería:

• A way to organize data
  • Examples
    • To-do list
    • Gift lists
    • Grocery Lists
• Items in list have position
• Items may be added anywhere
  • Write/modify items at a position.

Array Lists

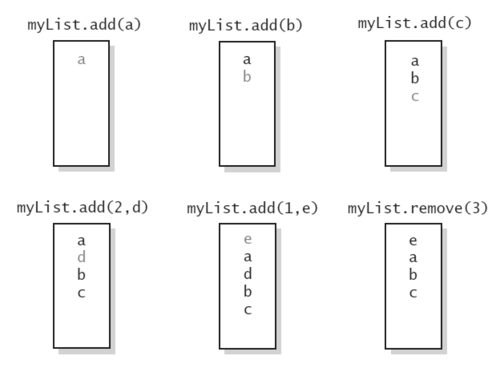
An obvious choice for implementing the list ADT is to use an array, A, where A[i] stores (a reference to) the element with index i. With a representation based on an array A, the get(i) and set(i, e) methods are easy to implement by accessing A[i] (assuming i is a legitimate index).

• Adding an Entry:
  • As we already saw on Arrays, in an operation add(i,o), we need to make room for the new element by shifting forward the n - i elements A[i],..., A[n - 1]
  • In the worst case (i = 0), this takes Order n time [O(n) times]
  • In an add operation, when the array is full, instead of throwing an exception, we can replace the array with a larger one.

• Removing an Entry:
  • In an operation remove(i), we need to fill the hole left by the removed element by shifting backward the n - i - 1 elements A[i + 1],..., A[n - 1]
  • In the worst case (i = 0), this takes O(n) time

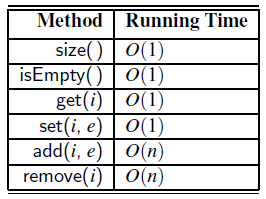
• Performance:
  • In an array-based implementation of a dynamic list:
    • The space used by the data structure is O(n)
    • Indexing the element at i takes O(1) time
    • add and remove run in O(n) time

The Linked List Data Structure

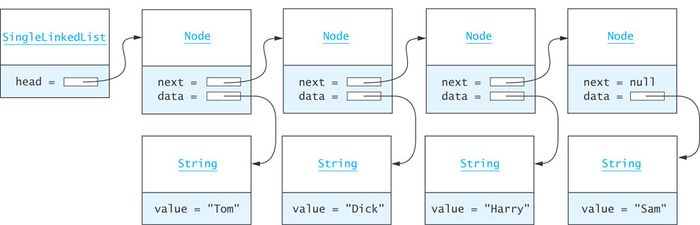
Single-Linked Lists

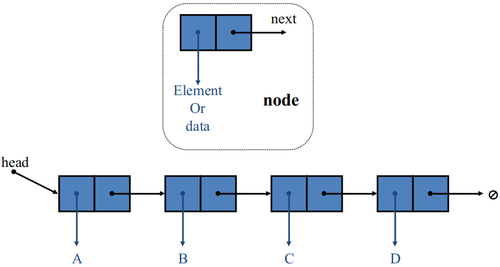
• A singly linked list is a concrete data structure consisting of a sequence of nodes, starting from a head pointer.
• Each node stores
  • Element or data
  • Link (reference or address) to the next node

• The ArrayList is limited because its add and remove methods operate in linear (O(n)) time—requiring a loop to shift elements.
• A linked list is useful for inserting and removing at arbitrary locations
  • In a linked list, instead of an index, each element is linked to the following element
  • A linked list can add and remove elements at a known location in O(1) time

Implementing a Single-Linked List in Java

NodeInterface.java

// Data Structures and Algorithms
// CCT College Dublin
// Dr. Muhammad Iqbal


public interface NodeInterface <E> {
    public void addFirst(E item);
    public void addAfter(Node<E> node, E item);
    
    public E removeFirst();
    public E removeAfter(Node<E> node);
    
    public Node<E> getNode(int index);
    
    public E get(int index);
    public E set(int index, E newValue);
    
    
    public void add(int index, E item);
    public boolean add(E item);
    
    public E remove(int index);
    public boolean remove(E item);
    
    public int size();
    
}

Node.java

// Data Structures and Algorithms
// CCT College Dublin
// Dr. Muhammad Iqbal


public class Node<E> {

    /** The data value. */
    public E data;
    /** The link */
    public Node<E> next = null;

    /**
     * Construct a node with the given data value and link
     * @param data - The data value 
     * @param next - The link
     */
    public Node(E data, Node<E> next) {
        this.data = data;
        this.next = next;
    }

    /**
     * Construct a node with the given data value
     * @param data - The data value 
     */
    public Node(E data) {
        this(data, null);
    }
}

SingleLinkedList.java

// Data Structures and Algorithms
// CCT College Dublin
// Dr. Muhammad Iqbal

public class SingleLinkedList<E> implements NodeInterface<E> {

    public Node<E> head = null;
    /** The size of the list */
    private int size = 0;

    // Helper Methods
    /** Insert an item as the first item of the list.
     *	@param item The item to be inserted
     */
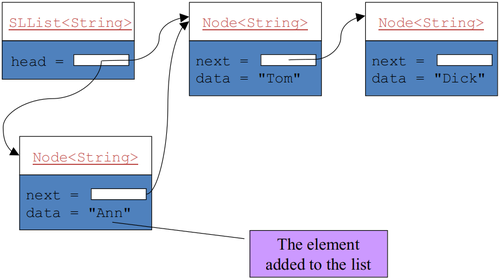
    public void addFirst(E item) {
        head = new Node<E>(item, head);
        size++;
    }

    /**
     * Add a node after a given node
     * @param node The node which the new item is inserted after
     * @param item The item to insert
     */
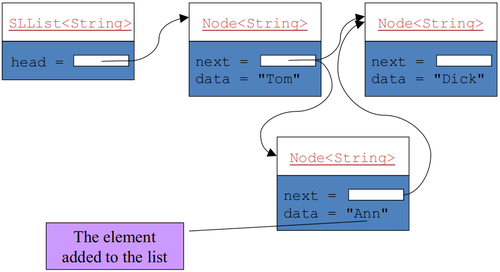
    public void addAfter(Node<E> node, E item) {
        node.next = new Node<E>(item, node.next);
        size++;
    }

    /**
     * Remove the first node from the list
     * @returns The removed node's data or null if the list is empty
     */
    public E removeFirst() {
        Node<E> temp = head;
        if (head != null) {
            head = head.next;
        }
        if (temp != null) {
            size--;
            return temp.data;
        } else {
            return null;
        }
    }

    /**
     * Remove the node after a given node
     * @param node The node before the one to be removed
     * @returns The data from the removed node, or null
     *          if there is no node to remove
     */
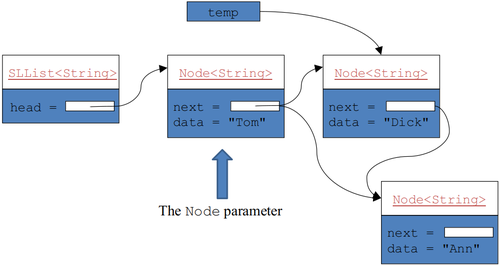
    public E removeAfter(Node<E> node) {
        Node<E> temp = node.next;
        if (temp != null) {
            node.next = temp.next;
            size--;
            return temp.data;
        } else {
            return null;
        }
    }

    /**
     * Find the node at a specified index
     * @param index The index of the node sought
     * @returns The node at index or null if it does not exist
     */
    public Node<E> getNode(int index) {
        Node<E> node = head;
        for (int i = 0; i < index && node != null; i++) {
            node = node.next;
        }
        return node;
    }

    // Public Methods
    /**
     * Get the data value at index
     * @param index The index of the element to return
     * @returns The data at index
     * @throws IndexOutOfBoundsException if the index is out of range
     */
    public E get(int index) {
        if (index < 0 || index >= size) {
            throw new IndexOutOfBoundsException(Integer.toString(index));
        }
        Node<E> node = getNode(index);
        return node.data;
    }

    /**
     * Set the data value at index
     * @param index The index of the item to change
     * @param newValue The new value
     * @returns The data value priviously at index
     * @throws IndexOutOfBoundsException if the index is out of range
     */
    public E set(int index, E newValue) {
        if (index < 0 || index >= size) {
            throw new IndexOutOfBoundsException(Integer.toString(index));
        }
        Node<E> node = getNode(index);
        E result = node.data;
        node.data = newValue;
        return result;
    }

    /**
     * Insert the specified item at the specified position in the list.
     * Shifts the element currently at that position (if any) and any
     * subsequent elements to the right (adds one to their indicies)
     * @param index Index at which the specified item is to be inserted
     * @param item The item to be inserted
     * @throws IndexOutOfBoundsException if the index is out of range
     */
    public void add(int index, E item) {
        if (index < 0 || index > size) {
            throw new IndexOutOfBoundsException(Integer.toString(index));
        }
        if (index == 0) {
            addFirst(item);
        } else {
            Node<E> node = getNode(index - 1);
            addAfter(node, item);
        }
    }

    /**
     * Append the specified item to the end of the list
     * @param item The item to be appended
     * @returns true (as specified by the Collection interface)
     */
    public boolean add(E item) {
        add(size, item);
        return true;
    }

    /*<exercise chapter="2" section="5" type="programming" number="1">*/
    /**
     * Remove the item at the specified position in the list. Shifts
     * any squsequent items to the left (subtracts one from their
     * indicies). Returns the tiem that was removed.
     * @param index The index of the item to be removed
     * @returns The item that was at the specified position
     * @throws IndexOutOfBoundsException if the index is out of range
     */
    public E remove(int index) {
        if (index < 0 || index >= size) {
            throw new IndexOutOfBoundsException(Integer.toString(index));
        }
        Node<E> removedNode = null;
        if (index == 0) {
            return removeFirst();
        } else {
            Node<E> node = getNode(index - 1);
            return removeAfter(node);
        }
    }
    /*</exercise>*/

    /**
     * Query the size of the list
     * @return The number of objects in the list
     */
    public int size() {
        return size;
    }

    /**
     * Obtain a string representation of the list
     * @return A String representation of the list 
     */
    @Override
    public String toString() {
        StringBuilder sb = new StringBuilder("[");
        Node p = head;
        if (p != null) {
            while (p.next != null) {
                sb.append(p.data.toString());
                sb.append(" ==> ");
                p = p.next;
            }
            sb.append(p.data.toString());
        }
        sb.append("]");
        return sb.toString();
    }

    /*<exercise chapter="2" section="5" type="programming" number="3">*/
    /**
     * Remove the first occurence of element item.
     * @param item The item to be removed
     * @return true if item is found and removed; otherwise, return false.
     */
    public boolean remove(E item) {
        if (head == null) {
            return false;
        }
        Node<E> current = head;
        if (item.equals(current.data)) {
            removeFirst();
            return true;
        }
        while (current.next != null) {
            if (item.equals(current.next.data)) {
                removeAfter(current);
                return true;
            }
            current = current.next;
        }
        return false;
    }
}

SingleLinkedList.addFirst

SingleLinkedList.addAfter

SingleLinkedList.removeAftert

SingleLinkedList.removeFirst

SLLTest.java

// Data Structures and Algorithms
// CCT College Dublin
// Dr. Muhammad Iqbal


public class SLLTest {

    /**
     * @param args the command line arguments
     */
    public static void main(String[] args) {
        Node<String> tom = new Node<String>("Tom");
        Node<String> dick = new Node<String>("Dick");
        Node<String> harry = new Node<String>("Harry");
        Node<String> sam = new Node<String>("Sam");

        tom.next = dick;
        dick.next = harry;
        harry.next = sam;
        
        SingleLinkedList<String> testInstance = new SingleLinkedList<String>();
        testInstance.add("Tom");
        testInstance.add("Dick");
        testInstance.add("Harry");
        testInstance.add("Berry");
        testInstance.add(4, "Peter");
        
        for (int i = 0; i < testInstance.size(); i++)
           {
             System.out.println("Linked List Values are " + testInstance.get(i));
           }
        
        testInstance.remove("Harry");
        testInstance.remove(1);
        testInstance.removeFirst();
        testInstance.toString();
        System.out.println("Linked List Values are " + testInstance.toString());
        
    for (int i = 0; i < testInstance.size(); i++)
        {
            System.out.println("Value are " + testInstance.get(i));
        }
        
    }
    
}

Double-Linked Lists

The Tree Data Structure

• Trees are nonlinear and hierarchical

• Tree nodes can have multiple successors (but only one predecessor)

• Trees can represent hierarchical organizations of information:
  • Class hierarchy
  • Disk directory and subdirectories
  • Family tree

• Trees are recursive data structures because they can be defined recursively

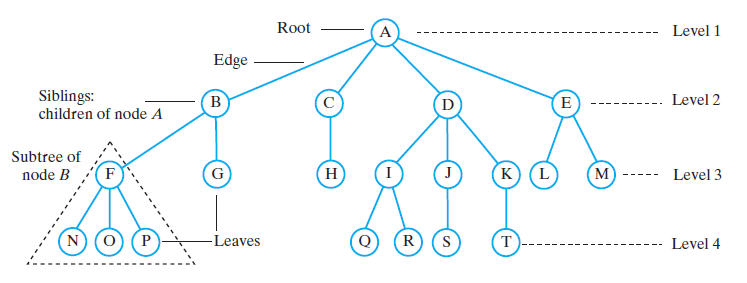
• A tree is comprised of a set of nodes in which elements are stored and edges connect one node to another. Each node is located on a particular level.

• A node can have only one parent, but may have multiple children. Nodes at the lower level of a tree are the children of nodes at the previous level.

• Nodes that have the same parent are siblings.

• The root is the only node which has no parent.

• A node that has no children is a leaf node.

• A node that is not the root and has at least one child is an internal node.

• A subtree is a tree structure that makes up part of another tree.

• We can follow a path through a tree from parent to child, starting at the root.

• A node is an ancestor of another node if it is above it on the path from the root.

• Nodes that can be reached by following a path from a particular node are the descendants of that node

• The level of a node is the length of the path from the root to the node

• The path length is the number of edges followed to get from the root to the node

• The height of a tree is the length of the longest path from the root to a leaf

• In computer science, a tree is an abstract model of a hierarchical structure

• A tree consists of nodes with a parent-child relation

• Applications:

• Organization charts
• File systems
• Programming environments

• Tree Terminology:

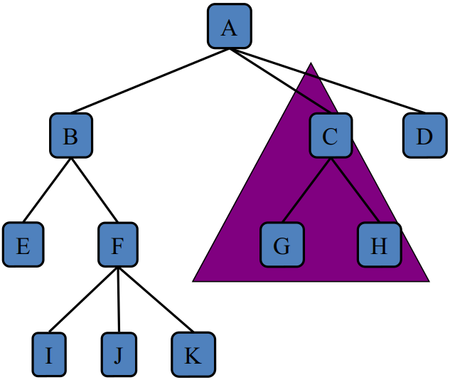
• Root: node without parent (A)
• Internal node: node with at least one child (A, B, C, F)
• External node (a.k.a. leaf ): node without children (E, I, J, K, G, H, D)
• Ancestors of a node: parent, grandparent, grand-grandparent, etc.
• Depth of a node: The depth of a node is the number of edges from the node to the tree's root node.
• Height of a tree: The height of a node is the number of edges on the longest path from the node to a leaf.
• Descendant of a node: child, grandchild, grand-grandchild, etc.
• Subtree: tree consisting of a node and its descendants

• Which nodes are the leaves?

• Which nodes are the siblings of node K?

• Which nodes are the children of node B?

• Which nodes are the descendants of node B?

• Which nodes are the ancestors of node N?

• Which nodes are parents?

Bubble and Insertion Sort

Sorting is the process of arranging a group of items into a defined order based on particular criteria.

Stable Sorting

• Stable sort algorithms sort identical elements in the same order that they appear in the input.
• In stable sorting, only part of the data is examined when determining the sort order.

Bubble Sort

https://liveexample.pearsoncmg.com/dsanimation/BubbleSortNeweBook.html

• Bubble sort orders a list of values by repetitively comparing neighboring elements and swapping their positions if necessary.
  • The sort algorithm starts from one end (the beginning), compares 2 adjacent data elements, and swaps them if they are in the wrong order.
  • It moves on down the list and continues doing so.
  • When it reaches the end of the data, it starts over until all the data is in the right order.

• Not much use in the real world, but is a great learning tool because it’s easy to understand and fast to implement.

• Use when a fast algorithm is needed to sort:

• An extremely small set of data (For example: Trying to get the books on a library shelf back in order.)
• A nearly sorted set of data. (Ex. Trying to decide which laptop to buy, because it is easier to compare pairs of laptops one at a time and decide which you prefer, than to look at them all at once and decide which was best.)

• Not Suitable:

• When dealing with a large set of data.
• When you are looking for a quick algorithm.
• Compared to other sorting algorithm, bubble sort is really slow.

Pseudo code for Bubble Sort

Method BubbleSort()
    Outer Loop: i to n
        Inner Loop: j from 0 to n - 1
           if a[j] > a[j + 1]
              swap( a[j], a[j + 1] )
end Method

Method Swap(A[J], A[J + 1])
    Temp = A(J)
    A(J) = A(J + 1)
    A(J + 1) = Temp
end

Complexity (Big O) of Bubble Sort Algorithm